|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
|
import sys
input = sys.stdin.readline
def DP(end) :
for i in range(2, end+1) :
TF0, TF1, TF2 = False, False, False
if l1[i-1] + l1[i] <= w :
TF1 = True
OXct = 1
OOctXO = 2
else :
OXct = 2
OOctXO = 3
if l2[i-1] + l2[i] <= w :
TF2 = True
XOct = 1
OOctOX = 2
else :
XOct = 2
OOctOX = 3
OOctOO = 2
if l1[i] + l2[i] <= w :
OOctOO = 1
OOctOX = 2
OOctXO = 2
DPOO[i] = min(DPOO[i-1] + OOctOO, DPOX[i-1] + OOctOX, DPXO[i-1] + OOctXO)
if max(DPOO[1], DPOX[1], DPXO[1]) == 5 :
TF0 = True
if TF1 and TF2 and (not TF0 or i > 2) :
DPOO[i] = min(DPOO[i], DPOO[i-2] + 2)
DPOX[i] = min(DPOO[i-1] + 1, DPOX[i-1] + 2, DPXO[i-1] + OXct)
DPXO[i] = min(DPOO[i-1] + 1, DPOX[i-1] + XOct, DPXO[i-1] + 2)
testcase = int(input())
for t in range(testcase) :
n, w = map(int, input().split())
l1 = [0] + list(map(int, input().split()))
l2 = [0] + list(map(int, input().split()))
if n == 1 :
if l1[1] + l2[1] <= w :
print(1)
else :
print(2)
continue
DPOO = [0 for i in range(n + 1)]
DPOX = [0 for i in range(n + 1)]
DPXO = [0 for i in range(n + 1)]
if l1[1] + l2[1] <= w :
DPOO[1] = 1
else :
DPOO[1] = 2
DPOX[1] = 1
DPXO[1] = 1
DP(n)
minw = DPOO[n]
if l1[-1] + l1[1] <= w :
DPOO = [0 for i in range(n + 1)]
DPOX = [0 for i in range(n + 1)]
DPXO = [0 for i in range(n + 1)]
DPOO[1] = 2
DPOX[1] = 1
DPXO[1] = 5
DP(n)
minw = min(minw, DPXO[n])
if l2[-1] + l2[1] <= w :
DPOO = [0 for i in range(n + 1)]
DPOX = [0 for i in range(n + 1)]
DPXO = [0 for i in range(n + 1)]
DPOO[1] = 2
DPOX[1] = 5
DPXO[1] = 1
DP(n)
minw = min(minw, DPOX[n])
if l1[-1] + l1[1] <= w and l2[-1] + l2[1] <= w :
DPOO = [0 for i in range(n + 1)]
DPOX = [0 for i in range(n + 1)]
DPXO = [0 for i in range(n + 1)]
DPOO[1] = 2
DPOX[1] = 5
DPXO[1] = 5
DP(n-1)
minw = min(minw, DPOO[n-1])
print(minw)
|
cs |
IDEA
DPOO[i]는 l1과 l2의 i-1번째까지는 완전히 점령하고 i번째를 l1, l2 모두 점령했을때의 부대수이다.
DPOX[i]는 l1과 l2의 i-1번째까지는 완전히 점령하고 i번째를 l1만 점령했을때의 부대수이다.
DPXO[i]는 l1과 l2의 i-1번째까지는 완전히 점령하고 i번째를 l2만 점령했을때의 부대수이다.
그리고 DPOO, DPOX, DPXO [i]는 서로의 이전 값들과의 비교로 결정된다.
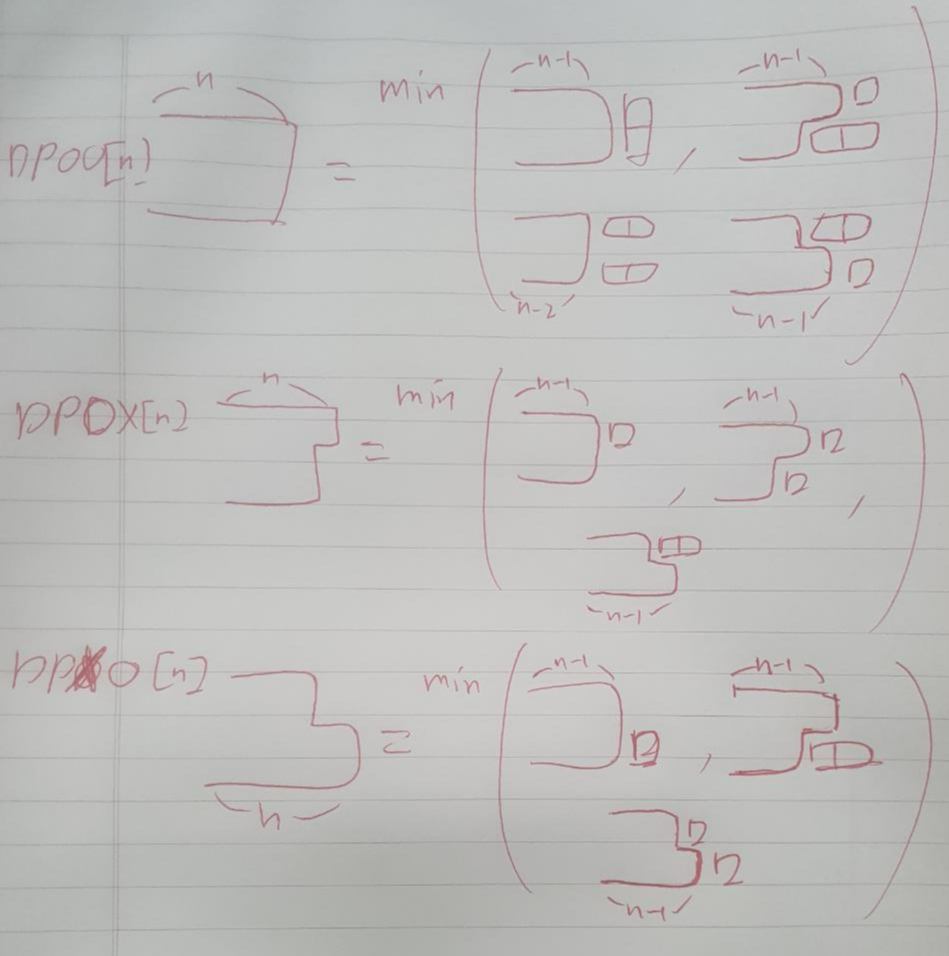
점화식을 식으로 표현하는 것보다 그림으로 표현하는 것이 이해가 빠를 것 같다.
이 그림의 점화식을 코드로 구현하면 된다. (line 4 ~ 33)
필드가 1번째와 -1번째가 연결된 고리형태이므로, 각 DP의 1번째는 초기 가정에 따라 수동으로 정해줘야 한다.
line 47 ~ 57
l1, l2 모두 끝점이 시작점과 연결되지 않았을 경우, l1[1], l2[1]과 w의 비교에 따른 초기값을 입력 후 DP를 채운다.
l1, l2 모두 끝점까지 채워야 하므로 DPOO[n]이 우리가 원하는 부대수이다.
line 59 ~ 77
l1만 끝점이 시작점과 연결된 경우, DPXO[1]은 불가능하므로(l1[1]이 이미 끝점과 연결되었으므로 X일수 없다)
초기값으로 DPXO[1] = 5 (불가능한 큰 값)을 입력 후 DP를 채운다.
시작점과 연결된 l1의 끝점은 비워야 하므로 DPXO[n]이 우리가 원하는 부대수이다.
l2만 끝점이 시작점과 연결된 경우, DPOX[1]은 불가능하므로
초기값으로 DPOX[1] = 5를 입력 후 DP를 채운다.
시작점과 연결된 l2의 끝점은 비워야 하므로 DPOX[n]이 우리가 원하는 부대수이다.
line 79 ~ 87
l1, l2 모두 끝점이 시작점과 연결된 경우, 시작점의 l1, l2 [1]의 값과 관계 없이 이미 두 부대를 시작점에 썼다.
따라서 DPOO[1] = 2, DPOX[1], DPXO[1] = 5이다. (이미 두 시작점에 부대가 차있으므로 XO, OX는 불가능하다)
시작점과 연결된 l1, l2의 끝점을 둘 다 비워야 하므로, DPOO[n-1]이 우리가 원하는 부대수이다.
line 57, 67, 77, 87
위의 네 경우를 취합해서 가장 작은 값이 최소 부대수이다.
이게 1트가 되네
'Week 01 ~ 04 : 알고리즘 문제 풀이' 카테고리의 다른 글
| 파이썬 백준 9249 최장 공통 부분 문자열 (0) | 2021.11.29 |
|---|---|
| 파이썬 백준 1700 멀티탭 스케줄링 (0) | 2021.11.27 |
| 파이썬 백준 1946 신입 사원 (0) | 2021.11.27 |
| 파이썬 백준 1931 회의실 배정 (0) | 2021.11.27 |
| 파이썬 백준 1541 잃어버린 괄호 (0) | 2021.11.27 |