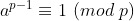
p가 소수라면, (p의 배수가 아닌) 모든 a에 대해 a^(p-1)은 mod p에서 1과 합동이다.
증명은 수학적귀납법으로 간단히 가능하니 패스 (위키에 있다)
정수론에서 C뿌리기를 당한 나도 다시보니 바로 기억날 만큼 유명한 정리인데, PS에서는 조합론적 문제에 이용할 수 있고 이 테크닉이 매우 흥미롭다.
팩토리얼이나 지수승을 주로 다루는 조합론은 자연스럽게 매우 큰 수들을 다루게 되는데, 컴퓨터를 이용한 계산에서는 보통 적당히 큰 수로 나눈 나머지를 다루는 모듈러 연산으로 합의를 본다.
이때 문제가 되는 것이 Combination, Permutation 등인데, 팩토리얼이 분모에 오는 위의 개념들은 팩토리얼의 실제 값 대신 모듈러 연산의 나머지를 쓰니 계산 결과가 실제 값과 틀리게 된다.
그런데 이때 그 '적당히 큰 수'를 1,000,000,007과 같은 소수로 정한다면, FlT에 의해 분모의 팩토리얼을 분자로 옮길 수가 있다. (다른 말로, 모듈러 곱셈의 역원을 취할 수 있다)
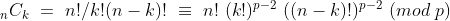
a^(p-1)이 1과 합동이므로, a^(p-2)가 a^-1과 합동이다. 따라서 분모에 있는 k!, (n-k)!을 각각의 p-2승으로 치환할 수 있게 된다.
이렇게 분자로 올린 팩토리얼의 p-2승은 큰 수의 거듭제곱을 연산하는 알고리즘과 함께 이용되어, 정확한 Combination, Permutation의 모듈러값을 구할 수 있게 된다.
위의 개념을 PS에 응용해서 풀 수 있는 문제의 예는 아래가 있다.
11401 이항 계수 3 (https://www.acmicpc.net/problem/11401)
13977 이항 계수와 쿼리 (https://www.acmicpc.net/problem/13977)
한편 소수의 성질을 다룬 정리이므로, 당연히 소수 이슈에도 엮인다.
하지만 FlT는 소수의 필요조건일 뿐 위를 만족한다고 소수인걸 보장하진 않는다. 자신과 서로소인 모든 a에 대해 위의 식을 만족하지만 소수가 아닌 수를 카마이클 수라고 부른다. 이를 이용한 문제도 몇 있다.
13319 가짜 소수 (https://www.acmicpc.net/problem/13319)
4223 가짜소수(https://www.acmicpc.net/problem/4233)
그렇다고 아예 소수 판별에 쓸모가 없는건 또 아니라서, 확률적 접근으로 "아마도 소수일 것 같다"는 판별을 할 수는 있다. 많은 테스트케이스로 검증할수록 소수일 확률이 높아지는 셈. 쉽게 구현할 수 있는 알고리즘 중 하나로 밀러 라빈 소수판정법이 있다.
근데 관련 문제들은 왠지 다 다이아다. 꿀통냄새가 나니 시간이 나면 파봐야겠다.
'알고리즘 개념 정리' 카테고리의 다른 글
| [소인수분해] 폴라드 로 알고리즘 (Pollard's rho) (0) | 2021.12.18 |
|---|---|
| [소수 판정] 밀러-라빈 알고리즘 (Miller-Rabin primality test) (0) | 2021.12.10 |
| [문자열] 맨버 마이어스 알고리즘 (0) | 2021.11.29 |
| DAC(분할 정복)과 비교해보는 DP(동적 계획) (0) | 2021.11.26 |
| 정렬 알고리즘 (0) | 2021.11.10 |