풀캠정글러

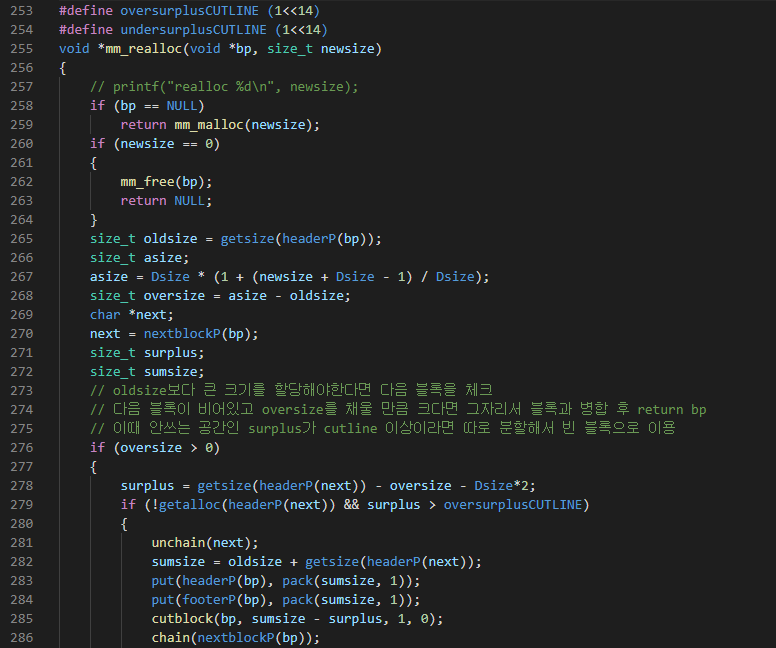
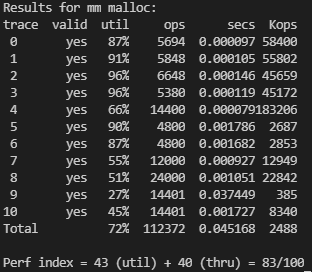
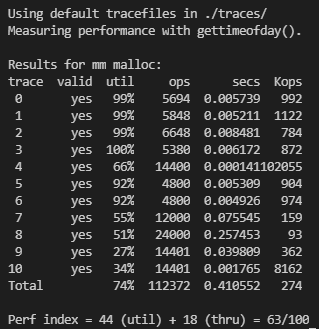
3. realloc 커스텀 (+5점) 기존의 realloc 함수는 bp의 위치와 기존, 새 size에 관계없이 새로 malloc을 실행 후 데이터를 복사하는 방식이었다. 하지만 realloc하려는 bp의 컨디션에 따라 무의미한 복사를 하지 않고도 재할당이 가능한 경우가 있어 이 경우 예외적으로 malloc을 재실행하지 않는다면, 새로 free되어 생기는 공간활용의 구멍도, malloc 실행에 쓰이는 연산력도 절약할 수 있다. newsize가 oldsize보다 크지만 bp의 다음 블록이 그 차이를 채울만큼 큰 빈 블록인 경우, newsize가 oldsize보다 작아서 제자리에서 재할당이 가능한 경우의 두 케이스에 대해 각각의 상황에 맞는 예외적인 절차를 밟도록 구현했다. Explicit 방식에 위의 몇가지..

1. CHUNKsize 축소 (+2점) malloc lab에서 다루는 heap의 사이즈는 20MB로 작고, 테스트케이스에서 할당과 free를 요구하는 용량도 작다. 이런 상황에서 extend_heap의 최소용량인 CHUNKsize가 4kB인건 비효율적인 공간 사용이 될 수 있다. CHUNKsize를 줄여가며 점수를 확인한 결과 2^8 이하일때 최대 점수가 나왔다. 2^7, 2^6 혹은 그 이하를 해도 점수가 더 오르진 않는걸 보면 너무 작은 용량은 테스트케이스에 없는 것 같다. 2. place 함수 커스텀 (+2점) place함수는 find_fit으로 선택된 빈 블록의 크기과 실제 할당을 요구한 크기의 차 surplus가 Dsize*2 이상이라면 그 나머지를 다시 빈 블록으로 분할하여 재활용한다. 기존의..

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 12..

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 12..

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 // Implicit과 공통되는 선언부 생략 static char *lastplacedP; static size_t lastplacedsize; int mm_init(void) // Implicit과 동일 static char *extend_heap(size_t words) // Implicit과 동일 static char ..

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 12..

1. Implicit을 채용한 malloc 구현 2. first fit을 next fit으로 개선 3. Explicit을 채용한 malloc 구현 4. Simple segregated을 채용한 malloc 구현 5. Buddy memory allocation을 채용한 malloc 구현

페르마의 소정리를 이용한 큰 수의 모듈러 연산 역원 찾기 (combination 계산에 이용) https://uneducatedjungler.tistory.com/120 밀러 라빈 알고리즘을 이용한 소수 판별 (큰 수에서는 확률적, 1e15 이하 작은 수에서는 확정적 판별 가능) https://uneducatedjungler.tistory.com/121 폴라드 로 알고리즘을 이용한 소인수분해 (유사난수와의 비교로 구한 랜덤인수를 밀러 라빈으로 소수 판별) https://uneducatedjungler.tistory.com/133 오일러 피 함수 (소인수분해를 이용한 빠른 계산) class 6에 정수론 관련 문제가 좀 있어 이쪽을 파다보니 조금 깊게 들어간 것 같다. 풀 수 있는 P1~D4 문제가 몇개 생..

페르마의 소정리(https://uneducatedjungler.tistory.com/120)에서 이어지는 글 n이 소수라면 (n의 배수가 아닌) 모든 a에 대해 위 식을 만족한다는 것이 페르마의 소정리이다. 즉, 어떤 단 하나의 a에 대해서라도 위 식을 만족하지 못함이 발견된다면, p는 100% 소수가 아니게 된다. 이에 확률론적으로 접근하면, p가 많은 수의 a에 대해 위 식을 만족할수록 p가 소수일 확률이 높아진다. 페르마 계열의 소수판별법은 여럿이 있는데, 요약하면 다음과 같다. n이 소수라면 위 식을 만족할테니, 충분히 많은 아무 a나 넣어보며 위 식을 만족하는지 확인하자. 한번이라도 만족을 안함이 발견되면 n은 소수가 아니다. break and return False 테스트를 다 통과하면 p는 ..

p가 소수라면, (p의 배수가 아닌) 모든 a에 대해 a^(p-1)은 mod p에서 1과 합동이다. 증명은 수학적귀납법으로 간단히 가능하니 패스 (위키에 있다) 정수론에서 C뿌리기를 당한 나도 다시보니 바로 기억날 만큼 유명한 정리인데, PS에서는 조합론적 문제에 이용할 수 있고 이 테크닉이 매우 흥미롭다. 팩토리얼이나 지수승을 주로 다루는 조합론은 자연스럽게 매우 큰 수들을 다루게 되는데, 컴퓨터를 이용한 계산에서는 보통 적당히 큰 수로 나눈 나머지를 다루는 모듈러 연산으로 합의를 본다. 이때 문제가 되는 것이 Combination, Permutation 등인데, 팩토리얼이 분모에 오는 위의 개념들은 팩토리얼의 실제 값 대신 모듈러 연산의 나머지를 쓰니 계산 결과가 실제 값과 틀리게 된다. 그런데 이때..